Solar power at a critical mass

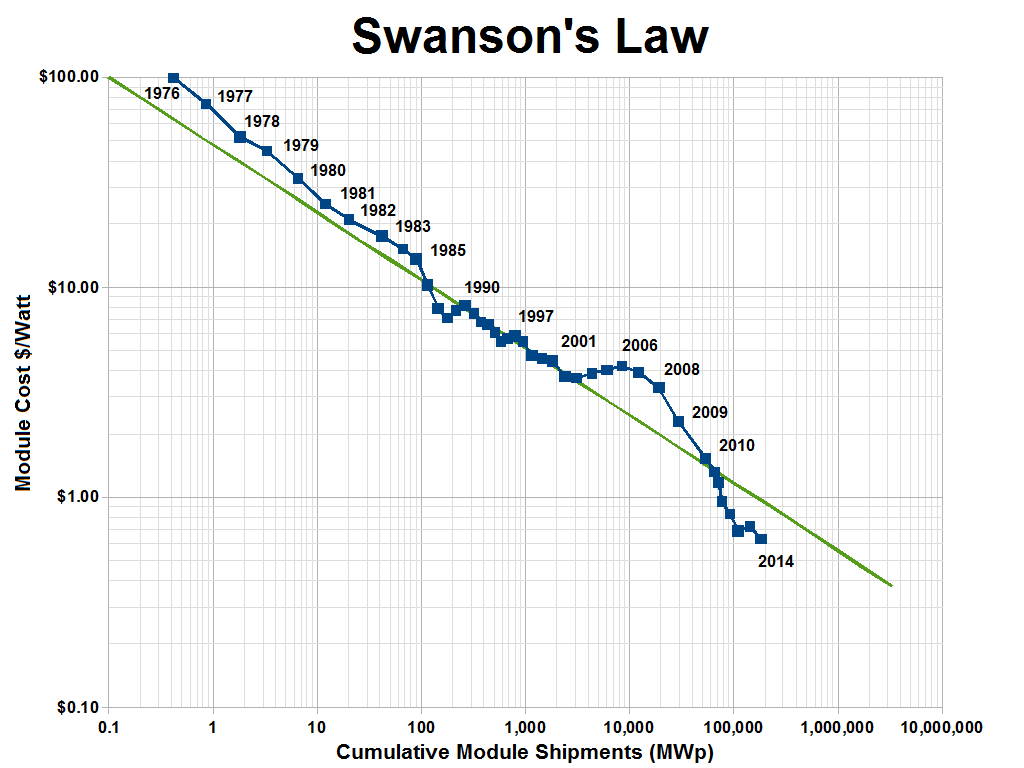
I've been reading science news, and I noticed that photovoltaic systems are rapidly becoming cheaper, and new PV solar power plants are constantly being built all over the world. This seems to be mostly the effect of pure economics - solar power is becoming competitive with coal/gas in many areas - than from governmental incentives or environmental considerations. From Wikipedia, we have a plot of PV cost vs year, showing a "Moore's Law"-type decrease every year, which is apparently called "Swanson's Law":

I'm not sure who tried to make that green line fit with the blue data but it doesn't look like a good fit. It seems like the cost is decreasing even faster than the original estimate of being cut in half every ten years. So how has that affected the total installed solar power capacity?

You can see that installed PV capacity, as a share of global electricity capacity, is increasing exponentially for now (sigmoidally once it has a significant percentage). My (very) simple and optimistic model predicts that half of all global electricity will be solar power by 2025. Ten years is a very short amount of time to go from less than 1% to more than 50%, so I would take this prediction with a big grain of salt. Some reasons why this model may be way off:

1. People are installing PV in the sunniest places with the highest energy costs, basically going after the lowest-hanging fruit. Once those places are saturated with PV, it'll be harder to convince people in cloudier places and with abundant fossil fuels to start investing in solar power. I'm sure there's an economic model of this phenomenon somewhere, but for now I'll defer to this headache-inducing technology adoption curve, which shows how disruptive technologies like electricity, refrigerators, clothes washers, autos, ACs, and internets are adopted over time. The main difference between these appliances/services and solar power is, anyone can install a few solar panels and sell electricity to their neighbors, but you can't easily opt-out of using solar electricity if your neighbor or utility company is providing that.
2. Economies of scale get tricky here. On the one hand, as we study this system and build more of these things, we get better and more efficient at doing it, making the process cheaper per panel. On the other hand, building a lot of these panels will start to impact the availability of raw materials necessary for them, like tellurium (required for a certain type of PV) or lithium (required to store the energy from PV until people want to use it).
3. Sunlight only shines during the day, and more in the summer than the winter. So once a certain area has enough PV to provide all daytime electricity demand, it won't be very useful to add any more PV unless there's some way to store that energy (like with batteries).
4. There's a large up-front cost for making changes, like shifting from coal to solar power. Your state might save $20M per year by building a solar power plant, but if you don't have the $100M to build it, and you do still have a fully operational coal power plant, then which one are you going to use? 
5. One huge source of carbon emissions that isn't included in the above chart is transportation fuels, primarily oil. Once electric cars have a comparable range to combustion cars, then cheap solar electricity may cause a widespread shift to electric vehicles. This might increase demand, but would also allow for that demand to be more flexible: You plug your car in when you arrive home, and you tell its nightrider-style computer, "buy electricity whenever it's cheapest, but make sure I have at least 50 miles of range by tomorrow morning". All the cars in your area will be doing the same thing, so when demand spikes or supply drops, they'll all pause, but when supply spikes or demand drops, they'll all start slurping those precious Amps. This will serve to help demand adapt to fit supply, keep the prices relatively steady, and keep electricity availability more stable. On top of that, those cars might further be programmed to "buy low and sell high", automatically selling energy back to the grid when it's expensive, earning their owners a few extra dollars a month, and further contorting electricity demand to more closely fit supply.
6. My sigmoidal model assumes that, eventually, all electricity will be made with solar power, but that's clearly not going to happen. For many cities and countries, it won't make sense to shut down their perfectly-good coal/nuclear/whatever plant until it breaks down. So I recalculated my fit to assume that solar power will only ever hit 60% of global electricity production, and the prediction is only delayed by three years: half of all electricity will be solar power by 2028. A quick note on the math here: since, as you can see in the semilog plot above, electricity has not left the "exponential" phase of the sigmoid shape - in other words, because it's so early and it only accounts for 0.9% of global supply - it's hard to predict where it will level off. I can get my model to fit with a correlation coefficient of 0.99 with a predicted maximum PV saturation as low as 3% of global supply. But we will know the answers within the next 5-10 years.

Case Study: Hawaii

Let's look a little closer at Hawaii, where expensive diesel-powered electricity and sunny days combine to make this electricity market a low hanging fruit for solar power. With 12% of all homes outfitted with PV, and solar power accounting for 4% of all electricity in 2013 by my estimate (including power produced and used by the same house, not just what goes over the grid), what's happening in Hawaii can help us understand what will happen with global PV.

The higher slope shows that Hawaii has more quickly adopted solar, because of all the factors which make solar so attractive there. (Data was hard to find here, so my data for 2012 and 2013 assumes that total power produced stayed the same as it was in 2011). My model suggests that solar should account for half of all power produced in Hawaii by 2018, which is breathtakingly sudden - but that model doesn't know about the bad news. There's been a big controversy about solar power on the islands, with the utility companies slowing down permits for residential installations, citing safety (the transmission lines, which were originally designed simply to deliver power from a few big sources to many small consumers, can't handle all the excess solar power generated during the day) while critics accuse the companies of protecting their own interests at the expense of residents. This has led to some people seceding from the grid, installing batteries to store their excess daytime energy for nighttime use. This is a taste of the barriers the rest of us will face in a few years, when local solar power production starts becoming significant. Can this be solved by simply installing a more robust power grid? Does each household need to buy a huge battery to help smooth out demand?

Regardless of these barriers, I'm still very excited about the near future of solar power.

New Mexico in Presidential politics

In this installment of the state-by-state series, I examine the newest Mexico there is, New Mexico. A relatively small state with relatively large swings in its margin of victory, to the intelligent human eye it seems to be somewhat unpredictable, with perhaps a chance of being a bit more democratic than the nation as a whole.

Democrats did better in New Mexico than in the nation as a whole in 5 of the last 7 presidential elections, and when they did worse, it was only by 1-2%. By contrast, when democrats did better in New Mexico than they did in the nation as a whole, they've lately been doing 6-10% better. This adds up to a prediction that democrats will do better in New Mexico than the nation as a whole by about 7.1% (based on my simple linear fit model). This is a close one, but I'm going to color it blue in our little map:

The Democrats seem to be doing well. However, keep in mind that in this map, blue and red are more like the projections of which party would win that state if the overall popular vote was at or near a tie. If one party has a large 4% advantage over the other, then a state like New Mexico, Nevada, Virginia, or North Carolina may well flip.

New Hampshire in presidential politics

Measurements of smaller populations should have larger uncertainty and error bars - and this is exactly what we see in New Hampshire, the smallest state to be covered so far on this blog series. Aside from a spectacular win by George H. W. Bush in 1988, New Hampshire has fluttered back and forth from republican-leaning in 1992 to democratic-leaning in 1996, back to the right in 2000, and finally back to the left for the following 3 elections since. I'll interpret this to mean that the Dukakis campaign probably abandoned all hope of winning there, and focused instead on other states. Subsequent campaigns probably focused more on New Hampshire, bringing it closer to the center.

We can see the somewhat ridiculous prediction by my naive linear model: an 8.9% advantage by the democrat, with rather large 4.6% error bars. Any real person looking at this data would predict that it'll probably be much closer, with perhaps a small democratic advantage (neglecting 1988 from my linear fit model - without any objective basis - gives a prediction of a smaller democratic advantage of 0.8-5.4%). My model could benefit from some way of weighting recent elections more heavily than long-ago elections. Maybe next time.

Coming up sometime soon (maybe) by popular demand: including the midterm election data in my prediction and analysis!

Arizona in Presidential Politics

Good old Arizona. I've seen a fair bit of interest on the left in a demographic advantage that Democrats my someday gain in Arizona (and other states, mostly in the South). So when I analyzed Arizona's margins in the last 7 elections, I was expecting to find some interesting wiggles and bounces. I was disappointed.

Aside from a small bounce for Republicans in 2008 (caused by hometown hero John McCain at the top of the ticket), Arizona has had little movement over the past 7 elections. In constructing my simple linear model, I excluded the 2008 data, and got a prediction that in 2016, Arizona will vote about 10% more republican than the nation as a whole. As it always has.

Blatantly screen-grabbing another website that lets me easily make my own little predicted map of the 2016 election, here's what we've got so far:

In this map I've shaded the states red or blue based on my guess as to whether or not a given party has a large advantage in that state. In other words, democrats won't necessarily win Pennsylvania, but if they've lost Pennsylvania, it will be because they've done very poorly in the national popular vote. As I visit each state on this blog, I'll fill in more states on this map, or leave them blank if they're true toss-up states. But as of right now, Democrats seem to be sitting pretty.

Astute readers will note that I have declared certain states without presenting a detailed analysis. For some of those states, I'll visit them in forthcoming posts. For others, I'll just let the history speak for itself (and if you want to gamble that Wyoming breaks blue, I'll take that bet).

Missouri: A Bellwether state from yesteryear

Until 2008, Missouri had the longest unbroken streak of electing the presidential candidate who ended up winning the presidency (although not always the popular vote). But during the last two cycles, Missouri abandoned its bellwether status, breaking toward the republicans even when Barack Obama won the national popular vote by more than seven points.

Starting in 1996, Missouri started drifting to the right of the nation as a whole, culminating in a 10% romp for Romney in 2012 while the nation voted for Obama by 4%. Based on my simple linear model, Missouri is almost certain to break for Republicans by a large margin.

Nevada in presidential politics

The next stop for our tour of possible swing states is Nevada.

We can see a pretty clear case of a state that has shifted somewhat from flirting with the republican party to flirting with the democratic party. Based on my extremely simple model, if this trend continues, Nevada has an 84% chance of voting at least 4.8% more democratic than the nation as a whole.

What might be causing this slow-and-steady shift to the left for Nevada? Perhaps an influx of minorities and young workers.

Kansas in Presidential Politics

Just a quick post that looks like all the others. Here I focus on Kansas, and how it has shifted from 5% more republican than the rest of the country, to reliably 25%+ more republican than the U.S. as a whole.

In contrast to the previous two states I've analyzed, Kansas clearly and definitively departed the "swing state" zone a long time ago. It's probable that neither party bothered to mount much of a campaign, causing Kansas to quickly shift to some kind of "natural state", the way it votes for president when it isn't a focus for both campaigns. And for Kansas, that natural state seems to be solid red.